LEY DE LOS EXPONENTES

Todas las "Leyes de los Exponentes" (o también "reglas de los exponentes") vienen de tres ideas:

El exponente de un número dice multiplica el número por sí mismo tantas veces

Lo contrario de multiplicar es dividir, así que un exponente negativo significa dividir

Un exponente fraccionario como 1/n quiere decir hacer la raíz n-ésima:

Si entiendes esto, ¡entonces entiendes todos los exponentes!

Y todas las reglas que siguen se basan en esas ideas.

Leyes de los exponentes

Aquí están las leyes (las explicaciones están después):

Ley	Ejemplo
x¹ = x	6¹ = 6
x⁰ = 1	7⁰ = 1
x^-1 = 1/x	4^-1 = 1/4

x^mxⁿ = x^m+n	x²x³ = x²⁺³ = x⁵
x^m/xⁿ = x^m-n	x⁴/x² = x^4-2 = x²
(x^m)ⁿ = x^mn	(x²)³ = x^2×3 = x⁶
(xy)ⁿ = xⁿyⁿ	(xy)³ = x³y³
(x/y)ⁿ = xⁿ/yⁿ	(x/y)² = x² / y²
x^-n = 1/xⁿ	x^-3 = 1/x³

Explicaciones de las leyes

Las tres primeras leyes (x¹ = x, x⁰ = 1 y x^-1 = 1/x) son sólo parte de la sucesión natural de exponentes. Mira este ejemplo:

Ejemplo: potencias de 5
	... etc...
5²	1 × 5 × 5	25
5¹	1 × 5	5
5⁰	1	1
5^-1	1 ÷ 5	0.2
5^-2	1 ÷ 5 ÷ 5	0.04
	... etc...

verás que los exponentes positivos, cero y negativos son en realidad parte de un mismo patrón, es decir 5 veces más grande (o pequeño) cuando el exponente crece (o disminuye).

La ley que dice que x^mxⁿ = x^m+n

En x^mxⁿ, ¿cuántas veces multiplicas "x"? Respuesta: primero "m" veces, despuésotras "n" veces, en total "m+n" veces.

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

Así que x²x³ = x⁽²⁺³⁾ = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Como en el ejemplo anterior, ¿cuántas veces multiplicas "x"? Respuesta: "m" veces, después reduce eso"n" veces (porque estás dividiendo), en total "m-n" veces.

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

(Recuerda que x/x = 1, así que cada vez que hay una x "sobre la línea" y una "bajo la línea" puedes cancelarlas.)

Esta ley también te muestra por qué x⁰=1 :

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Primero multiplicas x "m" veces. Después tienes que hacer eso "n" veces, en total m×n veces.

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

Así que (x³)⁴ = x^3×4 = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Parecido al ejemplo anterior, sólo ordena las "x"s y las "y"s

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

La ley que dice que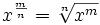

Para entenderlo, sólo recuerda de las fracciones que n/m = n × (1/m):

Ejemplo: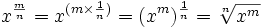

Y eso es todo

Si te cuesta recordar todas las leyes, acuérdate de esto: siempre puedes calcular todo si entiendes las tres ideas de la parte de arriba de esta página.

Ah, una cosa más... ¿Qué pasa si x= 0?

Exponente positivo (n>0)	0ⁿ = 0
Exponente negativo (n<0)	¡No definido! (Porque dividimos entre 0)
Exponente = 0	Ummm ... ¡lee más abajo!

El extraño caso de 0⁰

Hay dos argumentos diferentes sobre el valor correcto. 0⁰ podría ser 1, o quizás 0, así que alguna gente dice que es "indeterminado":

	x⁰ = 1, así que ...	0⁰ = 1
	0ⁿ = 0, así que ...	0⁰ = 0
	Cuando dudes...	0⁰ = "indeterminado"

SERIES Y SUCESIONES ARITMETICAS

Definición de sucesión aritmética

Una sucesión $a_{1}, a_{2},...,a_{n},...$ es una sucesión aritmética si hay un número real $d$ tal que para todo entero positivo $k$ ,

El número $d=a_{k+1}-a_{k}$ se le llama diferencial común de la sucesión.

Dada una sucesion aritmetica:

     k+1 = a+ d

para todo entero positivo K. Esto nos da una formula recursiva para encontrar terminos sucesivos .A partir de cualquier numero real a1. obtendremos una sucesion aritmetica con diferencia comun d con solo agregar d a a1, luego a a1+d y asi sucesivamente, con lo que resulta

Observa que la diferencia común $d$ es la diferencia de dos términos sucesivos cualesquiera de una sucesión aritmética.

El n-ésimo término de una sucesión aritmética

Teorema: fórmulas para $S_{n}$

Si $a_{1}, a_{2}, a_{3},...,a_{n},...$ es una sucesión aritmética con diferencia común $d$ , entonces la n-ésima suma parcial $S_{n}$ (esto es, la suma de los primeros $n$ términos), está dada por

Demostración

Podemos escribir
$S_{n}=a_{1}+a_{2} +a_{3} +...+a_{n}$
$=a_{1}+(a_{1}+d)+(a_{1}+2d)+...+[a_{1}+(n-1)d]$ .

Con el uso repetido de las propiedades conmutativa y asociativa de números reales resulta
$S_{n}=(a_{1}+a_{1}+a_{1}+...+a_{1})+[d+2d+...+(n-1)d]$ ,

con $a_{1} n$ veces dentro del primer par de paréntesis. Así
$Sn=na_{1}+d[1+2+...+(n-1)]$ .

La expresión dentro de corchetes es la suma de los primeros $n-1$ enteros positivos. Con la fórmula para la suma de los primeros $n$ enteros positivos, $S_{n}=n(n+1)/2$ , entonces tenemos

Sustituimos en la última ecuación por $S_{n}$ y factorizamos $n/2$ con lo cual

Puesto que $a_{n} = a_{1}+(n-1)d$ , la última ecuación es equivalente a

Historia de Gauss

LA maestra de Johann Carl Friedrich Gauss llego a dar la clase y les puso a todos sus alumnos un ejercicio en la pizarra que creía que les iba a llevar tiempo y podría descansar. El ejercicio era sumar los primeros 100 número enteros (del 1 al 100), pocos tiempo paso cuando Gauss dijo que habia terminado, la maestra pensó, "Deplano que no quiere trabajar"; su sorpresa fue que el ya habia resuelto el ejercicio, pero no solo eso sino que el resultado era correcto. La maestra le pregunto -¿como resolviste tan rápido el problema?- y el contesto -me di cuenta que si sumaba el ultimo con el primero (1+100) me daba 101, si sumaba el segundo con el penúltimo (2+99) también daba 101, y así sucesivamente hasta el 50 y 51 que también daban 101, así que lo que hice fue multiplicar 101*50; y así saque el resultado "5,050"-. Gauss solo tenia 10 años de edad.

SERIES Y SUCESIONES GEOMETRICAS

Sucesiones Geométricas

Definición de sucesión geométrica

Una sucesión $a_{1}, a_{2},..., a_{n},...$ es una sucesión geométrica si $a_{1} \neq 0$ y si hay un número real $r \neq 0$ tal que para todo entero positivo $k$ ,

El número $r = \frac{a_{k+1}}{a_{k}}$ se conoce la razón común de la sucesión.

Observa que la razón común $r = \frac{a_{k+1}}{a_{k}}$ es la razón entre dos términos sucesivos cualesquiera de una sucesión geométrica.

Formula para hallar el n-ésimo término de una sucesión geométrica

Teorema: fórmula para hallar $S_{n}$

La n-ésima suma parcial $S_{n}$ de una sucesión geométrica con primer término $a_{1}$ y razón común $r \neq 1 es$

Demostración

Por definición, la n-ésima suma parcial $S_{n}$ de una sucesión geométrica es

                                     . (1)

Si multiplicamos ambos lados de (1) por $r$ obtenemos

                                   . (2)

Si restamos la ecuación (2) de la (1), todos los términos de la derecha (con excepción de dos) se cancelan y obtenemos:

factorizar ambos miembros.

dividir entre (1-r)

Ejemplos

Ejemplo #1

Pruebe que la sucesión $a_{n}={(3n-1)}$ cuando n pertenece a los numeros Enteros es una sucesión aritmética.

$a_{k+1} - a_{k}= d$

$[3(k+1)-2] - [3_{k} - 2]= d$

$3_{k} + 3 - 2 - 3_{k} + 2 = d$
$3 = d$

$a_{1}, (a_{1}+ d), (a_{1}+2d), (a_{1} + 3d), ...$ .

$\sum a_{n}= a_{1} + (a_{1}+ d) + (a_{1}+2d) + ...$ .

$S_{1}= a_{1}$ ,
$S_{2}= a_{1} + (a_{1}+d) = 2a_{1} + d$
$S_{3}= (2a_{1}+d) + (a_{1}+2d) = 3a_{1} + 3d$
$S_{4}= (3a_{1} + 3d) + (a_{1} + 3d) = 4a_{1} + 6d$

$S_{5}= 5a_{1} + 10d$
$S_{6}= 6a_{1} + 15d$

$S_{n}= na_{1} + (n! + 1) d$

$S_{n}= na_{1} + \frac{n(n+1)}{2} == S_{n} = na_{1} + \frac{n(n-1)}{2}d$

Suma hasta el n-esimo término.

$S_{n}= \frac{n}{2}[2a_{1} + (n - 1)d]$

Generar el n-esimo término.

$a_{n}= a_{1} + (n -1)d$

--Dieguito 01:06 29 jul 2009 (UTC)

Ejemplo #2

Los tres primeros términos de una sucesión aritmética son $20, 16.5, 13, ...$ Encuentre el 15º término.

$16.5 - 20 = -3.5$

$a_{15}= 20 + 14(-3.5)$

$a_{15}= -29$

--Dieguito 01:06 29 jul 2009 (UTC)

Ejemplo #3

Si el cuarto término de una sucesión aritmética es 5 y el noveno es 20, indique el 6to término.

Identificamos $a_{n}$ conocidos, en este caso $a_{4}$ por ser el cuarto término y $a_{9}$ por ser el noveno termino.

$a_{4}= 5$ ------------> $a_{1} + 3d = 5$
$a_{9}= 20$ ----------> $a_{1} + 8d = 20$

Indentificamos el termino que queremos encontrar

$a_{6}= ?$

Operamos

$a_{1} = 5 - 3d$

$5-3d + 8d = 20$
$5 + 5d = 20$
$5d = 15$
$d = 3$

$a_{1} + 3(3)= 5$
$a_{1}= 5 - 9$
$a_{1}= -4$

Sustituimos en el termino que queremos encontrar, es decir, $a_{6}$

$a_{6} = -4 + 5(3)$

$a_{6} = 11$

Ejemplo #4

    Si la sucesión es 1,0.3,0.09,0.027.... es geométrica encuentre la suma de los primeros 5 términos.

a1=1 r=o.3

$S_{5}= 1-(0.3exp5)/1-0.3=1.4251$

MATEMATICAS 2°parcial

lunes, 30 de septiembre de 2013

LEY DE LOS EXPONENTES

Leyes de los exponentes

Explicaciones de las leyes

La ley que dice que x^mxⁿ = x^m+n

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

La ley que dice que

Ejemplo:

Y eso es todo

Ah, una cosa más... ¿Qué pasa si x= 0?

El extraño caso de 0⁰

SERIES Y SUCESIONES ARITMETICAS

Definición de sucesión aritmética

El n-ésimo término de una sucesión aritmética

Teorema: fórmulas para $S_{n}$

Demostración

Historia de Gauss

SERIES Y SUCESIONES GEOMETRICAS

Sucesiones Geométricas

Definición de sucesión geométrica

Formula para hallar el n-ésimo término de una sucesión geométrica

Teorema: fórmula para hallar $S_{n}$

Demostración

Ejemplos

Ejemplo #1

Ejemplo #2

Ejemplo #3

Ejemplo #4

lunes, 30 de septiembre de 2013

LEY DE LOS EXPONENTES

Leyes de los exponentes

Explicaciones de las leyes

La ley que dice que xmxn = xm+n

Ejemplo: x2x3 = (xx) × (xxx) = xxxxx = x5

La ley que dice que xm/xn = xm-n

Ejemplo: x4-2 = x4/x2 = (xxxx) / (xx) = xx = x2

Ejemplo: x2/x2 = x2-2 = x0 =1

La ley que dice que (xm)n = xmn

Ejemplo: (x3)4 = (xxx)4 = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x12

La ley que dice que (xy)n = xnyn

Ejemplo: (xy)3 = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x3y3

La ley que dice que (x/y)n = xn/yn

Ejemplo: (x/y)3 = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x3/y3

La ley que dice que

Ejemplo:

Y eso es todo

Ah, una cosa más... ¿Qué pasa si x= 0?

El extraño caso de 00

SERIES Y SUCESIONES ARITMETICAS

Definición de sucesión aritmética

El n-ésimo término de una sucesión aritmética

Teorema: fórmulas para

Demostración

Historia de Gauss

SERIES Y SUCESIONES GEOMETRICAS

Sucesiones Geométricas

Definición de sucesión geométrica

Formula para hallar el n-ésimo término de una sucesión geométrica

Teorema: fórmula para hallar

Demostración

Ejemplos

Ejemplo #1

Ejemplo #2

Ejemplo #3

Ejemplo #4

La ley que dice que x^mxⁿ = x^m+n

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

El extraño caso de 0⁰

Teorema: fórmulas para $S_{n}$

Teorema: fórmula para hallar $S_{n}$