En matemáticas , se define el máximo común divisor (abreviado mcd) de dos o más números enteros al mayor número que losdivide sin dejar resto. Por ejemplo, el mcd de 42 y 56 es 14. En efecto:
operando:
Siendo 3 y 4 primos entre sí (no existe ningún número natural, aparte de 1, que divida a la vez al 3 y al 4).
Precisiones
Si a y b son números enteros distintos de cero y si el número c es de modo que c|a y a su vez c|b, a este número c se denominadivisor común de los números a y b.1 Obsérvese que dos números enteros cualesquiera tienen divisores comunes. Ellos son 1 y -1. Cuando existen, únicamente, como divisores comunes 1 y -1 de los números a y b, estos se llaman primos entre sí.
Un número entero d se llama máximo común divisor (mcd) de los números a y b cuando: i) d es divisor común de los números a yb y ii) d es divisible por cualquier otro divisor común de los números a y b.
Como ejemplo, 12 es el mcd de 36 y 60. Pues 12|36 y 12|60; a su vez 12 es divisible por 1, -1, 2, -2, 4, -4, 6, -6, 12 y -12 que son divisores comunes de 36 y 60.2
Cálculo del mcd
Los dos métodos más utilizados para el cálculo del máximo común divisor de dos números son:
Por descomposición en factores primos
El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el mcd.
Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos
|
|
|
El MCD son los factores comunes con su menor exponente, esto es:
En la práctica, este método solo es operativo para números pequeños tomando en general demasiado tiempo calcular la descomposición en factores primos de dos números cualquiera.
Usando el algoritmo de Euclides
Un método más eficiente es el algoritmo de Euclides, que utiliza el algoritmo de la división junto al hecho que el mcd de dos números también divide al resto obtenido de dividir el mayor entre el más pequeño. Por ejemplo, si se divide 60 entre 48 dando un cociente de 1 y un resto de 12, el mcd será por tanto divisor de 12. Después se divide 48 entre 12 dando un resto de 0, lo que significa que 12 es el mcd. Formalmente puede describirse como:
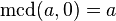

MCD de tres o más números
El máximo común divisor de tres números se puede calcular como sigue: , aunque hay métodos más prácticos y sencillos.
, aunque hay métodos más prácticos y sencillos.Propiedades
1. Si entonces
entonces  2. Si
2. Si es un entero,
es un entero, 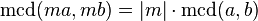 3. Si
3. Si es un número primo, entonces
es un número primo, entonces  o bien
o bien 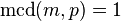 4. Si
4. Si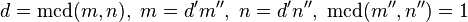 , entonces
, entonces 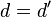 5. Si
5. Si es un divisor común de
es un divisor común de  y
y  , entonces
, entonces 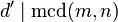 6. Si
6. Si , entonces
, entonces  7. Si
7. Si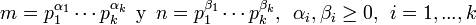 , entonces:La última propiedad indica que el máximo común divisor de dos números resulta ser el producto de sus factores primos comunes elevados al menor exponente.Geométricamente, el máximo común divisor de a y b es el número de puntos de coordenadas enteras que hay en el segmento que une los puntos (0,0) y (a,b), excluyendo el (0,0).
, entonces:La última propiedad indica que el máximo común divisor de dos números resulta ser el producto de sus factores primos comunes elevados al menor exponente.Geométricamente, el máximo común divisor de a y b es el número de puntos de coordenadas enteras que hay en el segmento que une los puntos (0,0) y (a,b), excluyendo el (0,0).Proposiciones
- Para cualquier par de números enteros a≠0, b≠0, existe un mcd. 3
- El m.c.d. de los números a y b puede ser representado en forma de combinación lineal de estos números.
- Si dos números enteros son primos entre sí, i.e. su mcd = 1 o en otra notación (a,b) = 1, entonces cabe la representación ma+ nb = 1 donde m y n son números enteros (Identidad de Bézout).
- si a|bc y (a,b) = 1, será a|c. En otras palabras, si un número a divide un producto de otros dos números y es coprimo con uno de ellos, entonces divide necesariamente el otro número o factor4 .
- Cuando un número a es coprimo con los números m y n, también lo es con el producto mn5 .
Aplicaciones
El mcd se utiliza para simplificar fracciones. Por ejemplo, para simplificar la fracción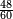 se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada
se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada  .El mcd también se utiliza para calcular el mínimo común múltiplo de dos números. En efecto, el producto de los dos números es igual al producto de su máximo común divisor por su mínimo común múltiplo. Así, para calcular el mínimo común múltiplo de 48 y de 60, calculamos primero su mcd, 12, siendo su mínimo común múltiplo
.El mcd también se utiliza para calcular el mínimo común múltiplo de dos números. En efecto, el producto de los dos números es igual al producto de su máximo común divisor por su mínimo común múltiplo. Así, para calcular el mínimo común múltiplo de 48 y de 60, calculamos primero su mcd, 12, siendo su mínimo común múltiplo .El mcd y el algoritmo de Euclides se emplea en la resolución de ecuaciones diofánticas lineales con dos incógnitas.6
.El mcd y el algoritmo de Euclides se emplea en la resolución de ecuaciones diofánticas lineales con dos incógnitas.6Referencias
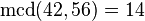




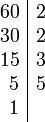
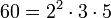
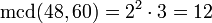


No hay comentarios:
Publicar un comentario