Convenios de notación
Puesto que los números naturales se utilizan para contar objetos, el cero puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de la ciencia, el conjunto de los números naturales puede presentarse entonces de dos maneras distintas:
|
donde la N de natural se suele escribir en "negrita de pizarra".
Históricamente, el uso del cero como numeral fue introducido en Europa en el siglo XII con la conquista musulmana de la península ibérica,1 pero no se consideraba un número natural.2
Sin embargo, con el desarrollo de la teoría de conjuntos en el siglo XIX, el cero se incluyó en las definiciones conjuntistas de los números naturales. Esta convención prevalece en dicha disciplina,3 y otras, como la teoría de la computación.4 En particular, el estándar DIN 5473 adopta esta definición.4 Sin embargo, en la actualidad ambos convenios conviven.5
Para distinguir ambas definiciones a veces se introducen símbolos distintos. Por ejemplo, si se incluye el cero en los naturales, al conjunto de los números naturales sin el cero se lo llama conjunto de los enteros positivos y se lo denota como  . Alternativamente también se utiliza
. Alternativamente también se utiliza  .6
.6
 . Alternativamente también se utiliza
. Alternativamente también se utiliza  .6
.6
Por el contrario, cuando el 0 no se considera un número natural (cosa que es conveniente, por ejemplo, en divisibilidad y teoría de números), al conjunto de los naturales con el cero se lo llama conjunto de los números cardinales y se lo denota  .
.
 .
.Historia
Antes de que surgieran los números para la representación de cantidades, el ser humano usó otros métodos para contar, utilizando para ello objetos como piedras, palitos de madera, nudos de cuerdas, o simplemente los dedos. Más adelante comenzaron a aparecer los símbolos gráficos como señales para contar, por ejemplo marcas en una vara o simplemente trazos específicos sobre la arena (Véase hueso de Ishango). Pero fue en Mesopotamia alrededor del año 4.000 a. C. donde aparecen los primeros vestigios de los números que consistieron en grabados de señales en formas de cuñas sobre pequeños tableros de arcilla empleando para ello un palito aguzado. De aquí el nombre de escritura cuneiforme. Este sistema de numeración fue adoptado más tarde, aunque con símbolos gráficos diferentes, en la Grecia Antigua y en la Antigua Roma. En la Grecia antigua se empleaban simplemente las letrasde su alfabeto, mientras que en la antigua Roma además de las letras, se utilizaron algunos símbolos.
Quien colocó al conjunto de los números naturales sobre lo que comenzaba a ser una base sólida, fue Richard Dedekind en el siglo XIX. Este los derivó de una serie de postulados (lo que implicaba que la existencia del conjunto de números naturales se daba por cierta), que después precisó Peano dentro de una lógica de segundo orden, resultando así los famosos cinco postulados que llevan su nombre. Frege fue superior a ambos, demostrando la existencia del sistema de números naturales partiendo de principios más fuertes. Lamentablemente la teoría de Frege perdió, por así decirlo, su credibilidad y hubo que buscar un nuevo método. Fue Zermeloquien demostró la existencia del conjunto de números naturales, dentro de su teoría de conjuntos y principalmente mediante el uso del axioma de infinitud que, con una modificación de este hecha por Adolf Fraenkel, permite construir el conjunto de números naturales como ordinales según von Neumann.
Algunas características de los números naturales son:
- Todo número mayor que 1 (o mayor que 0 en caso de considerar el 0 como natural) va después de otro número natural.
- Entre dos números naturales siempre hay un número finito de naturales. (Interpretación de conjunto no denso)
- Dado un número natural cualquiera, siempre existe otro natural mayor que éste. (Interpretación de conjunto infinito).
Construcciones axiomáticas
Históricamente, se han realizado propuestas para axiomatizar la noción habitual de números naturales, de entre las que destacan las de Peano, (Axiomas de Peano) y la construcción a partir de la teoría de conjuntos.
Axiomas de Peano
- Si n es un número natural, entonces el sucesor de n también es un número natural.
- El 1 no es el sucesor de ningún número natural.
- Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
- Si el 1 pertenece a un conjunto de números A, y además siempre se verifica que: dado un número natural cualquiera que esté enA, su sucesor también pertenece a A; entonces A contiene al conjunto de todos los números naturales. Este es el axioma de inducción, que captura la idea de inducción matemática.
Definición en teoría de conjuntos
En teoría de conjuntos se define al conjunto de los números naturales como el mínimo conjunto que es inductivo. La idea es que se pueda contar haciendo una biyección desde un número natural hasta el conjunto de objetos que se quiere contar. Es decir, para dar la definición de número 2, se requiere dar un ejemplo de un conjunto que contenga precisamente dos elementos. Esta definición fue proporcionada por Bertrand Russell, y más tarde simplificada por Von Neumann quien propuso que el candidato para 2 fuera el conjunto que contiene solo a 1 y a 0.
Formalmente, un conjunto  se dice que es un número natural si cumple
se dice que es un número natural si cumple
 se dice que es un número natural si cumple
se dice que es un número natural si cumple- Para cada
 ,
, 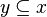
- La relación
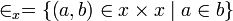 es un orden total estricto en
es un orden total estricto en 
- Todo subconjunto no vacío de
 tiene elementos mínimo y máximo en el orden
tiene elementos mínimo y máximo en el orden 
Se intenta pues, definir un conjunto de números naturales donde cada elemento respete las convenciones anteriores. Primero se busca un conjunto que sea el representante del 0, lo cual es fácil ya que sabemos que  no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
 no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
Se define-según Halmos- entonces que el conjunto vacío es un número natural que se denota por  y que cada número natural
y que cada número natural  tiene un sucesor denotado como
tiene un sucesor denotado como 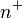 . Estas ideas quedan formalizadas mediante las siguientes expresiones:
. Estas ideas quedan formalizadas mediante las siguientes expresiones:
 y que cada número natural
y que cada número natural  tiene un sucesor denotado como
tiene un sucesor denotado como 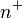 . Estas ideas quedan formalizadas mediante las siguientes expresiones:
. Estas ideas quedan formalizadas mediante las siguientes expresiones:
De esta manera, cada elemento de algún número natural es un número natural; a saber, un antecesor de él. Por ejemplo:
- Por definición
 (lo cual refuerza el hecho de que 0 no tiene antecesores)
(lo cual refuerza el hecho de que 0 no tiene antecesores) - 1 es el sucesor de 0, entonces

- 2 es el sucesor de 1, pero 1 es {0}, entonces
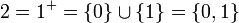
- y en general
Esto permite establecer una relación de orden entre los elementos del conjunto a pesar de que un conjunto es por naturaleza un agregado de elementos desordenados. Se define esta relación mediante la expresión
También se puede usar otra definición más inmediata a partir del hecho de que cada número natural consta de sus antecesores. Así  si y sólo si
si y sólo si  .
.
 si y sólo si
si y sólo si  .
.
Ésa es la construcción formal de los naturales que garantiza su existencia como conjunto a la luz del desarrollo axiomático Zermelo-Fraenkel. El postulado de los conjuntos infinitos asegura la validez de la técnica de demostración conocida como inducción matemática.
Un teorema demuestra que cualquier conjunto que sea inductivo contiene a todos los números naturales, es decir que si  es un conjunto inductivo, entonces
es un conjunto inductivo, entonces  . Esto significa que, en efecto,
. Esto significa que, en efecto,  es el mínimo conjunto inductivo.
es el mínimo conjunto inductivo.
 es un conjunto inductivo, entonces
es un conjunto inductivo, entonces  . Esto significa que, en efecto,
. Esto significa que, en efecto,  es el mínimo conjunto inductivo.
es el mínimo conjunto inductivo.
Lo que convierte a los números naturales  en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedad cancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedad cancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
 en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedad cancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedad cancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
De manera análoga, la multiplicación × se define mediante las expresiones
Esto convierte  (esto es, ℕ con esta nueva operación), en un monoide conmutativo.
(esto es, ℕ con esta nueva operación), en un monoide conmutativo.
 (esto es, ℕ con esta nueva operación), en un monoide conmutativo.
(esto es, ℕ con esta nueva operación), en un monoide conmutativo.
Otra forma de construcción de  es la siguiente: Sea
es la siguiente: Sea 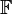 la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈
la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈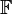 se dice que A R B
se dice que A R B  Existe una aplicación biyectiva de A sobre B,es decir,existe
Existe una aplicación biyectiva de A sobre B,es decir,existe  biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente
biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente ![\mathbb{F}/R\ = \{ [A] / A\in \mathbb{F} \}](http://upload.wikimedia.org/math/5/9/d/59d0f955deac98282b5cbf050f121c86.png) los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que
los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que  sea unsemianillo conmutativo y unitario.
sea unsemianillo conmutativo y unitario.
 es la siguiente: Sea
es la siguiente: Sea 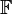 la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈
la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈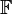 se dice que A R B
se dice que A R B  Existe una aplicación biyectiva de A sobre B,es decir,existe
Existe una aplicación biyectiva de A sobre B,es decir,existe  biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente
biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente ![\mathbb{F}/R\ = \{ [A] / A\in \mathbb{F} \}](http://upload.wikimedia.org/math/5/9/d/59d0f955deac98282b5cbf050f121c86.png) los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que
los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que  sea unsemianillo conmutativo y unitario.
sea unsemianillo conmutativo y unitario.Operaciones con los números naturales
Las operaciones matemáticas que se definen en el conjunto de los números naturales son la suma y la multiplicación.
La suma y la multiplicación de números naturales son operaciones conmutativas y asociativas, es decir:
- El orden de los números no altera el resultado (propiedad conmutativa), a+b = b+a, y a×b = b×a.
- Para sumar — o multiplicar — tres o más números naturales, no hace falta agrupar los números de una manera específica ya que (a+b)+c=a+(b+c) (propiedad asociativa). Esto es lo que da sentido a expresiones como a+b+c.
Al construir la operación de multiplicación de números naturales, se puede observar claramente que la adición o suma y la multiplicación son operaciones compatibles, pues la multiplicación sería una adición de cantidades iguales y gracias a esta compatibilidad se puede desarrollar la propiedad distributiva, que se expresa:
Aparte, estas dos operaciones cumplen con las propiedades de:
- Clausura de ambas operaciones para todos los números naturales a y b, ya que a + b y a × b son siempre números naturales.
- Existencia de elementos neutros para ambas operaciones, es decir, para cada número a, a + 0 = a y a × 1 = a.
- No existencia de divisores de cero para la operación de multiplicación: si a y b son números naturales tales que a × b = 0, entonces a = 0 ó b = 0.
Propiedades de los números naturales
Los números naturales están totalmente ordenados. La relación de orden  se puede redefinir así:
se puede redefinir así:  si y sólo si existe otro número natural
si y sólo si existe otro número natural  que cumple
que cumple  . Este orden es compatible con todas las operaciones aritméticas puesto que si
. Este orden es compatible con todas las operaciones aritméticas puesto que si  ,
,  y
y  son números naturales y
son números naturales y  , entonces se cumple:
, entonces se cumple:
 se puede redefinir así:
se puede redefinir así:  si y sólo si existe otro número natural
si y sólo si existe otro número natural  que cumple
que cumple  . Este orden es compatible con todas las operaciones aritméticas puesto que si
. Este orden es compatible con todas las operaciones aritméticas puesto que si  ,
,  y
y  son números naturales y
son números naturales y  , entonces se cumple:
, entonces se cumple:
Una propiedad importante del conjunto de los números naturales es que es un conjunto bien ordenado
- Para cualquier elemento a de A existe b en A tal que a < b
En los números naturales existe el algoritmo de la división. Dados dos números naturales a y b, si b≠ 0, podemos encontrar otros dos números naturales q y r, denominados cociente y resto respectivamente, tales que:
 y
y  .
.
Los números q y r están unívocamente determinados por a y b.
Otras propiedades más complejas de los números naturales, como la distribución de los números primos por ejemplo, son estudiadas por la teoría de números.
Uso de los números naturales
Los números naturales, son usados para dos propósitos fundamentalmente: para describir la posición de un elemento en una secuencia ordenada, como se generaliza con el concepto de número ordinal, y para especificar el tamaño de un conjunto finito, que a su vez se generaliza en el concepto de número cardinal (teoría de conjuntos). En el mundo de lo finito, ambos conceptos son coincidentes: los ordinales finitos son iguales a N así como los cardinales finitos. Cuando nos movemos más allá de lo finito, ambos conceptos son diferentes.
- Otro uso de gran importancia, desde el punto de vista matemático, es en la construcción de los números enteros, para lo cual enN×N se establece una relación de equivalencia, para dos pares ordenados de N×N:
- (a,b) ~ (c,d) si y solo si a + d = b + c.
Sustracción o resta con números naturales
Asúmase que ℕ = {0, 1, 2, 3,...} y sea H = {(m, n)/ m, n ∈ ℕ; m ≥ n}, sea g una aplicación de H en ℕ, tal que g(m,n)= m-n = d si solo si m = d + n, donde m,n están en H y d está en ℕ. A la aplicación g de H sobre ℕ se llama sustracción o resta en N. La diferencia d = m-n , sólo es posible en el caso que m ≥ n.
Proposiciones
- Si m - n = p, entonces m - p= n
- Si m - n = p, entonces (m +r) - ( n+ r) = p
- Para cualquier m ∈ ℕ, m - m = 0;
- como m- 0 = m , 0 hace el papel de elemento neutro por la derecha.
- La resta no es conmutativa ni asociativa.
- Si se da m - n = p, existe una infinidad de números naturales m´y m´tal que m´- n´= p; de modo tal que en ℕxℕ la relación (m,n) ≈ (m´,n´) s.s.s. m + n´ = n + m´ define una relación de equivalencia, punto de partida para la construcción del ℤ de los números enteros 7 .
EJERCICIOS:



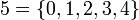


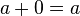

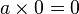








No hay comentarios:
Publicar un comentario