Cálculo del mínimo común múltiplo (m.c.m)
Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:
|
|
|
Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:
Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.
Propiedades básicas
- Si el producto de dos números lo dividimos por su máximo común divisor dicho cociente es el mínimo común múltiplo.
- A y B que descompuestos en números primos será A=(p1·p2)·p3·p4 y B=(p1·p2)·p5·p6 donde si m.c.d. es (p1·p2) y el producto de A·B=(p1·p2)·p3·p4·(p1·p2)·p5·p6 donde vemos que (p1·p2) está repetido dos veces, luego si dividimos ese total por (p1·p2) tendremos el total menor que contiene a A y B siendo su mcm
- El mínimo común múltiplo de dos números, donde el menor divide al mayor, será el mayor. Es lógico ya que un múltiplo de ambos inferior al mayor sería imposible ya que no sería múltiplo del mayor.
- El mínimo común múltiplo de dos números primos es el total de su multiplicación. Esto es lógico ya que su máximo común divisor es 1.
- El mínimo común múltiplo de dos números compuestos será igual al cociente entre su producto y el m.c.d de ellos. Es evidente según la propiedad 1 de este tema.
- El máximo común divisor de varios números está incluido en el mínimo común múltiplo.
Aplicaciones del mínimo común múltiplo
Suma de fracciones
Véase también: Mínimo común denominador.
Véase también: Fracción.
El mcm se puede emplear para sumar o restar fracciones de distinto denominador, tomando el mcm de los denominadores de las fracciones, y convirtiéndolas en fracciones equivalentes que puedan ser sumadas. Véase el siguiente ejemplo:
Para poder efectuar la suma, primero se debe buscar el mínimo común múltiplo de los denominadores (6 y 33)
|
|
|
luego el mínimo común múltiplo de 6 y 33 es:
que corresponde al número 66; ambas fracciones tendrán como denominador 66, ahora sólo hay que hallar a cada fracción su fracción equivalente, con denominador 66 y será posible la suma:
operando las fracciones, podemos realizar la suma:
Expresiones algebraicas
El m.c.m. para dos expresiones algebraicas, corresponde a la expresión algebraica de menor coeficiente numérico y de menor grado que es divisible exactamente por cada una de las expresiones dadas. Esta teoría es de suma importancia para las fracciones y ecuaciones.1
De esta forma el m.c.m. de 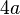 y
y  es
es  igualmente para
igualmente para  y
y  es
es 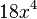 .
.
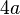 y
y  es
es  igualmente para
igualmente para  y
y  es
es 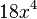 .
.Algoritmos de cálculo
Para más de dos números, un algoritmo es el siguiente:
- Descomponer los números en factores primos.
- Para cada factor, elegir entre todas las descomposiciones aquel factor con mayor exponente.
- Multiplicar todos los factores elegidos.
Por ejemplo, mcm(324,16,7,5) La descomposición de 324 es 22·34; la descomposición de 16 es: 24; la descomposición de 7 es 7 y la descomposición de 5 es 5. Por tanto, obtenemos el mcm: 24·34·7·5 = 45360.
EJERCICIOS:
Un faro se enciende cada 12 segundos, otro cada 18 segundos y un tercero cada minuto. A las 6.30 de la tarde los tres coinciden.
Averigua las veces que volverán a coincidir en los cinco minutos siguientes.
Debemos tener todos los tiempos en la misma unidad, por ejemplo en segundos.
12 = 22 · 3
18 = 2 · 32
60 = 22 · 3 · 5
m. c. m. (12 , 18, 60) = 22 · 32 · 5 = 180
180 : 60 = 3 Coinciden cada 3 minutos, por tanto en los 5 minutos siguientes sólo coinciden una vez.
Sólo a las 6.33 h.
Solución del ejercicio 2
Un viajero va a Barcelona cada 18 días y otro cada 24 días. Hoy han estado los dos en Barcelona.
¿Dentro de cuantos días volverán a estar los dos a la vez en Barcelona?
18 = 2 · 32
24 = 23 · 3
m. c. m. (18, 24) =23 · 32 = 72
Dentro de 72 días.
Solución del ejercicio 3
¿Cuál es el menor número que al dividirlo separadamente por 15, 20, 36 y 48, en cada caso, da resto 9?
m. c. m. (15, 20, 36, 48) = 24 · 32 · 5 = 720
720 + 9 = 729
Solución del ejercicio 4
En una bodega hay 3 toneles de vino, cuyas capacidades son: 250 l, 360 l, y 540 l. Su contenido se quiere envasar en cierto número de garrafas iguales. Calcular las capacidades máximas de estas garrafas para que en ellas se pueda envasar el vino contenido en cada uno de los toneles, y el número de garrafas que se necesitan.
m. c. d. (250, 360, 540) = 10
Capacidad de las garrafas = 10 l.
Número de garrafas de T1 = 250/10 = 25
Número de garrafas de T2 = 360/10 = 36
Número de garrafas de T3 = 540/10 = 54
Número de garrafas = 25 + 36 + 54 = 115 garrafas.
Solución del ejercicio 5
El suelo de una habitación, que se quiere embaldosar, tiene 5 m de largo y 3 m de ancho.
Calcula el lado de la baldosa y el número de la baldosas, tal que el número de baldosas que se coloque sea mínimo y que no sea necesario cortar ninguna de ellas.
Como las baldosas se suelen medir en centímetros, pasamos todo a centímetros.
3 m = 300 cm = 2² · 3 · 5²
5 m = 500 cm = 2² · 5³
A = 300 · 500 = 150000 cm2
m. c. d. (300, 500) = 2² · 5² = 100 cm de lado
Ab = 1002 = 10000 cm2
150000 : 10000 = 15 baldosas
Solución del ejercicio 6
Un comerciante desea poner en cajas 12 028 manzanas y 12 772 naranjas, de modo que cada caja contenga el mismo número de manzanas o de naranjas y, además, el mayor número posible. Hallar el número de naranjas de cada caja y el número de cajas necesarias.
Calculamos el máximo común divisor.
12 028 = 2² · 31 · 97
12 772 = 2² · 31 · 103
m. c. d. (12 028, 12 772) = 124
124 naranjas en cada caja.
Cajas de naranjas = 12 772 / 124 = 103
Cajas de manzanas = 12 028 / 124 = 97
Cajas necesarias = 103 + 97 = 200

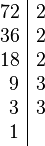
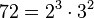
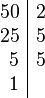

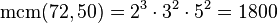
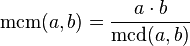








ola :v
ResponderEliminark ace :v toi solito :''v aiuda